하드 드라이브에 대한 액세스를 다시 얻는 방법, 하드 드라이브를 열 수 없는 오류 수정

이 글에서는 하드 드라이브에 문제가 생겼을 때 다시 접근할 수 있는 방법을 안내해 드리겠습니다. 함께 따라 해 보세요!
정삼각형, 직각삼각형, 이등변삼각형의 넓이를 계산하는 공식은 무엇인가요 ? 삼각형의 면적을 계산하는 가장 쉽고 일반적으로 사용되는 방법을 알아보려면 아래 기사를 참조하세요.
목차
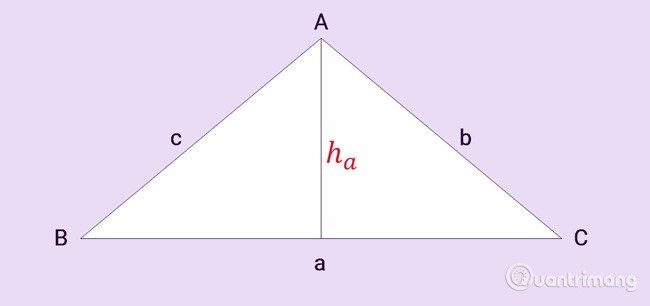
삼각형 ABC에는 세 변 a, b, c가 있으며, ha는 그림과 같이 꼭짓점 A로부터의 높이입니다.
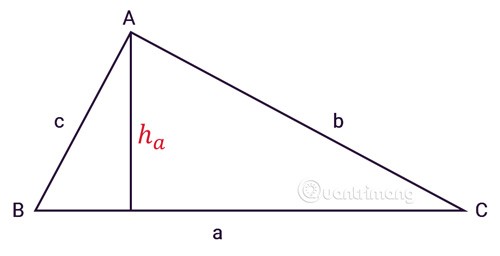
삼각형의 넓이는 높이에 대변(밑변)의 길이를 곱한 후 2로 나눈 값과 같습니다.
정삼각형의 면적 계산에 관한 시
삼각형의 넓이는 쉽습니다.
높이에 밑변을 곱한 후 절반으로 나눕니다.
예를 들어:
밑변의 길이가 5m, 높이가 24dm인 삼각형의 면적을 계산해 보세요.
해결책: 높이 24dm = 2.4m
삼각형의 면적은 다음과 같습니다.
삼각형의 넓이는 삼각형의 두 인접한 변의 곱의 절반에 두 변이 이루는 각의 사인을 곱한 값과 같습니다.
예를 들어:
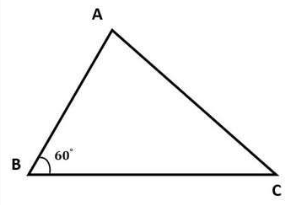
삼각형 ABC의 변 BC는 7, 변 AB는 5, 각 B는 60도이다. 삼각형 ABC의 넓이를 계산해 보세요?
상:
검증된 Heron 공식을 사용하면:
p가 삼각형의 반둘레일 때:
다음 공식을 사용하여 다시 쓸 수 있습니다.
예를 들어:
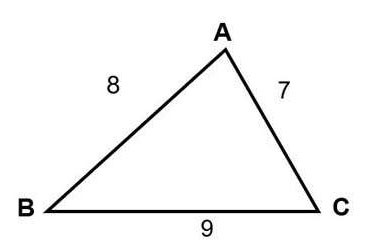
변의 길이가 AB = 8, AC = 7, CB = 9인 삼각형의 면적을 계산하세요.
상:
삼각형 ABC의 반둘레는
우리가 가지고 있는 영웅 공식을 적용하면
다른:
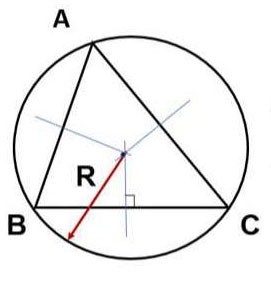
참고사항: 삼각형을 외접하는 원의 반지름이 R임을 증명해야 합니다.
예를 들어:
삼각형 ABC가 주어졌을 때, 변의 길이는 a = 6, b = 7, c = 5, R = 3입니다. (R은 삼각형 ABC를 외접하는 원의 반지름입니다.) 삼각형 ABC의 넓이를 계산해 보세요.
상:

예를 들어: 삼각형 ABC의 각 변의 길이 AB = 20, AC = 21, BC = 15, r = 5(r은 삼각형 ABC에 내접하는 원의 반지름)를 알고 있을 때 삼각형 ABC의 넓이를 계산합니다.
상:
삼각형의 반둘레는 다음과 같습니다.
r=5
삼각형의 면적은 다음과 같습니다.
이등변 삼각형은 정삼각형과 같습니다. 위와 같이 높이에 밑변을 곱한 다음 2로 나누는 공식을 적용할 수 있습니다. 더욱 복잡한 고급 공식도 있습니다.
이등변 삼각형 ABC는 세 개의 변을 가지고 있으며, a는 밑변의 길이이고, b는 두 변의 길이이며, ha는 그림과 같이 꼭짓점 A로부터의 높이입니다.
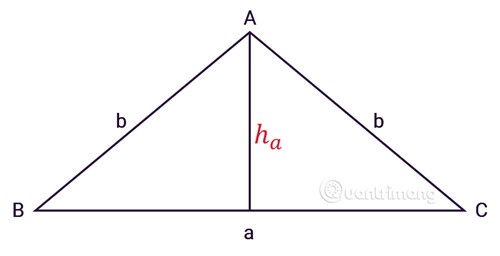
정삼각형의 면적을 계산하는 공식을 적용하면 이등변삼각형의 면적을 계산하는 공식이 있습니다.
정삼각형 ABC는 세 개의 같은 변을 가지고 있으며, 그림과 같이 변의 길이를 a라고 합니다.
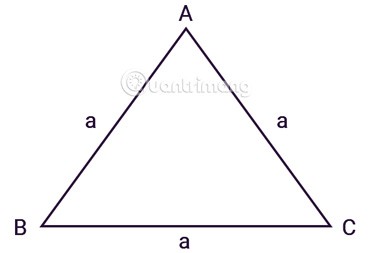
헤론의 정리를 적용하여 추론하면 정삼각형의 면적을 계산하는 공식은 다음과 같습니다.
삼각형 ABC는 B에서 직각을 이루고 있으며, a, b는 두 직각변의 길이입니다.
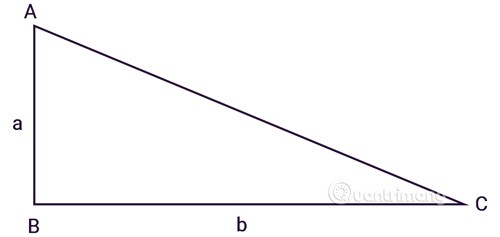
두 직각변 중 하나를 높이로 하고 나머지 한 변을 밑변으로 하는 직각 삼각형의 넓이를 계산하는 공식을 적용해 보세요.
직각 삼각형의 면적을 계산하는 공식:
직각 삼각형의 면적을 계산하는 것에 대한 시:
두 개의 직각을 가진 삼각형.
침착함을 유지하고, 당황하지 말고, 실수하지 마세요.
측면, 측면을 곱하고 2로 나누면
면적이 됩니다. 빠르게 연습하세요.
삼각형 ABC는 A에서 직각삼각형이고, a는 두 변의 길이입니다.
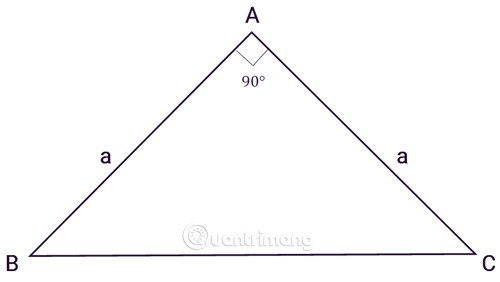
직각 삼각형의 면적을 계산하는 공식을 높이와 밑변이 같은 직각 이등변 삼각형의 면적에 적용하면 다음 공식을 얻습니다.
이론적으로 위의 공식을 사용하면 공간이나 옥시즈 공간에서 삼각형의 면적을 계산할 수 있습니다. 하지만 이렇게 하면 계산에 어려움이 생길 수 있습니다. 따라서 옥시즈 공간에서는 사람들이 방향곱을 사용하여 삼각형의 면적을 계산하는 경우가 많습니다.
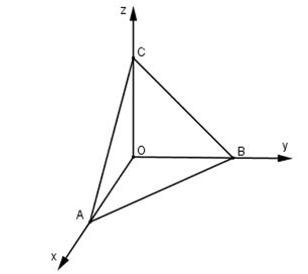
공간 Oxyz에서 삼각형 ABC가 주어졌습니다. 삼각형 ABC의 면적은 다음 공식으로 계산됩니다.
예 :
Oxyz 공간에서 세 개의 꼭짓점 A(-1;1;2), B(1;2;3), C(3;-2;0)의 좌표를 갖는 삼각형 ABC가 주어졌습니다. 삼각형 ABC의 넓이를 계산해 보세요.
해결책 :
우리는 가지고 있습니다:
삼각형의 면적을 계산하려면 삼각형의 종류를 파악해야 하며, 이를 바탕으로 올바른 면적 계산 공식과 삼각형의 면적을 가능한 한 빨리 계산하는 데 필요한 요소를 찾아야 합니다.
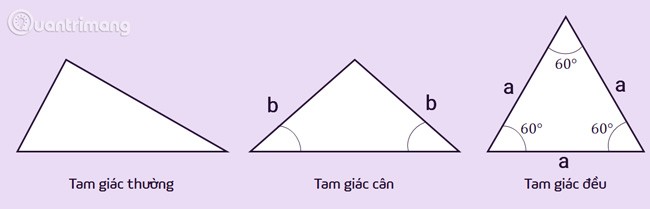
정삼각형: 가장 기본적인 삼각형으로, 변의 길이가 서로 다르고, 내각의 크기도 서로 다릅니다. 규칙적인 삼각형은 삼각형의 특수한 경우를 포함할 수도 있습니다.
이등변 삼각형: 두 변의 길이가 같은 삼각형으로, 이 두 변을 두 옆변이라고 합니다. 이등변 삼각형의 꼭짓점은 두 개의 인접한 변의 교차점입니다. 꼭짓점이 이루는 각을 꼭짓각이라 하고, 나머지 두 각을 밑각이라 합니다. 이등변 삼각형의 특징은 밑변의 두 각이 같다는 것입니다.
정삼각형: 세 변이 모두 같은 이등변 삼각형의 특수한 경우입니다. 정삼각형의 특징은 세 각의 크기가 같고 60도라는 것입니다.
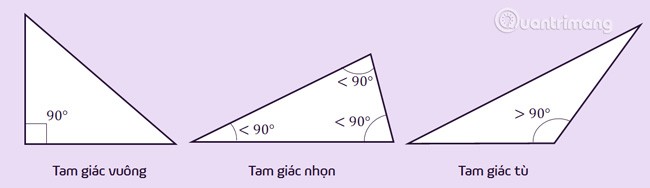
직각삼각형: 한 각이 90도인 삼각형(직각)입니다.
둔각삼각형: 내각이 90도보다 큰 삼각형(둔각)이거나 외각이 90도보다 작은 삼각형(예각)입니다.
예각삼각형: 세 개의 내각이 모두 90도보다 작은 삼각형(세 개의 예각)이거나 모든 외각이 90도보다 큰 삼각형(여섯 개의 둔각)입니다.
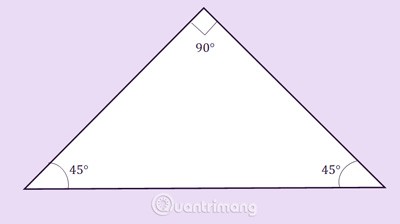
직각이등변삼각형: 직각삼각형이면서 이등변삼각형입니다.
위에는 일반적인 삼각형 면적 계산 공식을 요약하여 옥시즈 좌표계에서 삼각형 면적을 계산하는 방법을 설명했습니다. 문의사항, 질문 또는 의견이 있으시면 아래에 댓글을 남겨 Quantrimang.com과 논의해 주시기 바랍니다.
이 글에서는 하드 드라이브에 문제가 생겼을 때 다시 접근할 수 있는 방법을 안내해 드리겠습니다. 함께 따라 해 보세요!
AirPods는 언뜻 보기에 다른 무선 이어폰과 별반 다르지 않아 보입니다. 하지만 몇 가지 잘 알려지지 않은 기능이 발견되면서 모든 것이 달라졌습니다.
Apple은 iOS 26을 출시했습니다. 완전히 새로운 불투명 유리 디자인, 더욱 스마트해진 경험, 익숙한 앱의 개선 사항이 포함된 주요 업데이트입니다.
학생들은 학업을 위해 특정 유형의 노트북이 필요합니다. 선택한 전공 분야에서 뛰어난 성능을 발휘할 만큼 강력해야 할 뿐만 아니라, 하루 종일 휴대할 수 있을 만큼 작고 가벼워야 합니다.
Windows 10에 프린터를 추가하는 것은 간단하지만, 유선 장치의 경우와 무선 장치의 경우 프로세스가 다릅니다.
아시다시피 RAM은 컴퓨터에서 매우 중요한 하드웨어 부품으로, 데이터 처리를 위한 메모리 역할을 하며 노트북이나 PC의 속도를 결정하는 요소입니다. 아래 글에서는 WebTech360에서 Windows에서 소프트웨어를 사용하여 RAM 오류를 확인하는 몇 가지 방법을 소개합니다.
스마트 TV는 정말로 세상을 휩쓸었습니다. 이렇게 많은 뛰어난 기능과 인터넷 연결 덕분에 기술은 우리가 TV를 시청하는 방식을 바꾸어 놓았습니다.
냉장고는 가정에서 흔히 볼 수 있는 가전제품이다. 냉장고는 보통 2개의 칸으로 구성되어 있는데, 냉장실은 넓고 사용자가 열 때마다 자동으로 켜지는 조명이 있는 반면, 냉동실은 좁고 조명이 없습니다.
Wi-Fi 네트워크는 라우터, 대역폭, 간섭 외에도 여러 요인의 영향을 받지만 네트워크를 강화하는 몇 가지 스마트한 방법이 있습니다.
휴대폰에서 안정적인 iOS 16으로 돌아가려면 iOS 17을 제거하고 iOS 17에서 16으로 다운그레이드하는 기본 가이드는 다음과 같습니다.
요거트는 정말 좋은 음식이에요. 매일 요구르트를 먹는 것이 좋은가요? 매일 요구르트를 먹으면, 몸에 어떤 변화가 있을까요? 함께 알아보죠!
이 기사에서는 가장 영양가 있는 쌀 종류와 어떤 쌀을 선택하든 건강상의 이점을 극대화하는 방법에 대해 설명합니다.
수면 일정과 취침 루틴을 정하고, 알람 시계를 바꾸고, 식단을 조절하는 것은 더 나은 수면을 취하고 아침에 제때 일어나는 데 도움이 되는 몇 가지 방법입니다.
임대해 주세요! Landlord Sim은 iOS와 Android에서 플레이할 수 있는 모바일 시뮬레이션 게임입니다. 여러분은 아파트 단지의 집주인 역할을 하며 아파트 내부를 업그레이드하고 세입자가 입주할 수 있도록 준비하여 임대를 시작하게 됩니다.
욕실 타워 디펜스 Roblox 게임 코드를 받고 신나는 보상을 받으세요. 이들은 더 높은 데미지를 지닌 타워를 업그레이드하거나 잠금 해제하는 데 도움이 됩니다.













